What are Quantum Gates?
When starting out in quantum computing, you will invariably encounter the phrase: “quantum gate.” To underwhat what a quantum gate is, we first discuss the context these gates are used in. Strap in, because we’re about to dive head first into a crash course on basic quantum gates.
A quantum computer stores information in quantum bits, or qubits. These bits may be in some superposition of two states, |0⟩ and |1⟩ (that is, there is some probability of measuring the value of the bit as being |0⟩ and some probability of measuring the value of the state as being |1⟩).
Mathematically, these states can be represented as vectors.
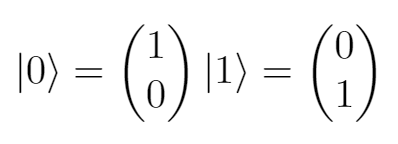
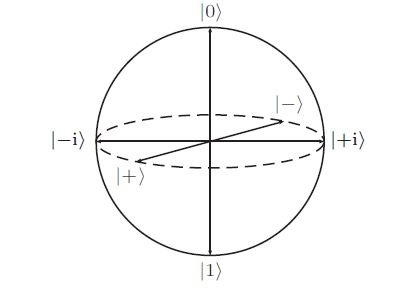
These vectors then correspond to locations on the Bloch sphere, the latter of which is a visual representation of all the possible states of a qubit.
Note that any angles when represented in quantum computing are done in radians, where a 90° rotation corresponds to 𝛑/2 radians, a 180° rotation corresponds to 𝛑 radians, and so on.
| Degrees (°) | Radians (rad) |
| 0° | 0 rad |
| 90° | 𝛑/2 rad |
| 180° | 𝛑 rad |
| 270° | 3𝛑/2 rad |
| 360° | 2𝛑 rad |
The most common examples of a state in superposition are the |+⟩ and |-⟩ states, where there is exactly a 1/2 chance of measuring a qubit in either the |0⟩ or the |1⟩ states. Mathematically, they can be represented as a linear combination of these two fundamental states, as follows.
and
What are quantum gates?
Quantum gates are ways we can perform operations on these qubits. The objective of a quantum computer is to be able to make a computation of some sort. These computations are represented by chances in the values – or states – of the bits.
For gates that are applied to only one qubit at a time, this can be represented by flips of states or rotations around some X, Y, or Z axis on the Bloch sphere. For gates applied to multiple qubits, the combinations can be considerably more complicated. In this crash course, we cover only the most basic gates to get you started.
Top Quantum Gates to Know
As with learning any new topic, we first begin by defining some notation. Quantum “gates” are to quantum circuits as logical gates are to propositions, or as regular circuit gates are to an electrical circuit. These gates, as previously mentioned, perform operations on the values of these bits, which are organized into a system called a circuit.
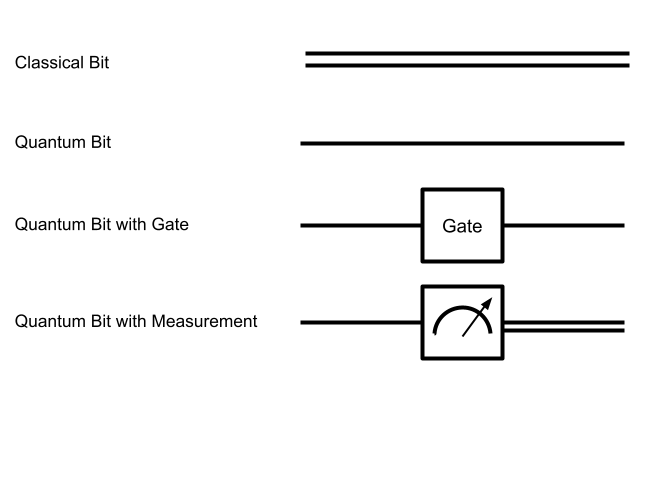
To visualize these operations, we can use what are known as circuit diagrams. We differentiate between classical bits – the typically 0 and 1 bits found in a computer – and qubits using the number of spacing of lines.
When a gate is applied to the bit, a “box” (like a machine that performs the given operation) is applied to the particular line. The word “gate” in the diagram can be replaced with a symbol or letter representing the gate – such as a “H” or “X”. A measurement collapses the state of the qubit into a singular value, which is saved on a classical bit, and thus a special symbol is used to denote this action.
Pauli Gates
Let us begin by revisiting the Bloch sphere. Observe that rotations may be made around the X, Y, and Z axes. When these rotations occur at an angle of 𝛑 radians, a special gate name is assigned. These are referred to as Pauli gates. Recall that we may express a state as a vector. When a gate is applied, we may write the gate as a matrix that is multiplied by the vector representing the qubit.

Note that the Pauli-X rotation gate is the same as a NOT gate (in classical computing). As such, it has a special symbol on top of the standard “X” gate symbol.
Applying Multiple Gates
What happens when a gate is applied multiple times? In the case of these rotation gates, it’s like rotating the the state of the qubit twice around the given axis – resulting in a full rotation of 2𝛑 radians – or 360 degrees.
As a result, applying any of the Pauli rotation gates twice is like applying what is known as an identity gate. When an identity gate is applied, it’s like applying no gate at all: the input state is equivalent to the output state.

More Rotation Gates
In some cases, the angle of rotation is further broken down or special combinations of rotations expressed using another gate name.
For example, the Hadamard gate is a 𝛑 radian rotation around the X-axis, followed by second 𝛑 radian rotation around the Y-axis. This pairing of actions results in a superposition where there is an exactly 1/2 chance of measuring the qubit in state 0 and a 1/2 chance of measuring the qubit to be in state 1. Rather than applying the Pauli-X and Pauli-Y rotations, the H-gate is defined instead.
The rotations may be more generally written as Rx, Ry, and Rz gates – or generally categorized under the name “Pauli gate”. In this specific case, we focus on the matrix for a phase shift around the Z-axis.. Just like with the 𝛑 radian rotations, there are special names for 𝛑/4 and 𝛑/8 radian phase rotations.
We briefly summarize these – and give their equivalent matrices – below.

As with before, applying S-gate is applied 4 times is equivalent to the Pauli-Z gate, and applying the S-gate 8 times is equivalent to the identity gate. Similarly, applying the T gate twice is equivalent to the S-gate, 8 times is equivalent to the Pauli-Z gate, and 16 times is equivalent to the identity gate.
Multi-Qubit Gates
We are also able to make the information on qubits “connected” to one another in some way. The most familiar of these is the CNOT gate, which also exists in classical computing.
In circuits, controlled gates have two parts: the control qubit(s) and the target qubit(s). The state of the control qubits will decide whether some gate is applied to the targets. In the case of the CNOT gate, the control qubits must be in the 1 state for a NOT gate to be applied to the singular target qubit.

More generally, a two-qubit control gate may be expressed as:

Any number of target and control qubits may be used, and most gates may be “triggered” by the controls.
There is one last multi-qubit gate you will commonly encounter, known as the SWAP gate. As the name implies, the SWAP gate swaps the states of the input qubits. While the operation seems rather redundant at the moment, it will become incredibly important when you begin to work on higher-level quantum projects, such as mapping your quantum circuit to real-life qubits.

Conclusion
While there is a laundry list of other quantum gates out there, this set of gates – such as the Hadamard, phase shift, CNOT, and T gate combination – can be used together to construct almost every useful gate needed to perform all operations on a circuit. This set of gates is called the Universal Set, since the universe of plausible gates can be built from only the gates in this set.
With that, we conclude this crash course on quantum gates. We briefly outlined what quantum circuits and gates are, and then highlighted key rotation and multi-qubit gates to take note of. Congratulations on surviving, and have fun delving deeper into quantum computing!