Superdense coding is a procedure that allows us to send two classical bits to another party using just a single qubit during communication. In a simplified way, this protocol replaces two classical bits with one qubit. In this tutorial we will gain a basic understanding of Super Dense Coding. We will understand the steps of the protocol using 2 qubits and finally implement the circuit initialized using 2 qubits in a simulator and real quantum device.
Steps Involved:
1. Preparation: Prepare (by convention) state; split the two pair among sender and receiver.
2. Transport: Sender physically moves away with h(is/er) pair of entangled qubit.
3. Encoding: Sender encodes classical bits of information to h(is/er) pair of qubit.
4. Transmission: Sender transmits h(is/er) qubit to receiver.
5. Decoding: Receiver decodes and measures h(is/er) qubit to retrieve sender's classical state.
It starts with a third party (say, Charlie) who prepares a pair of entangled states at |0⟩ Applying Hadamard gates to both the initialized qubits a CX gate is applied in order to create an entangled state. (First one as control and second one as the target).
def preparation(qc):
qc.h(0)
qc.cx(0,1)
Sender takes q0 and receiver takes q1, they travel far apart.
def seperation(qc):
qc.barrier()
Charlie sends the first qubit to sender and the second qubit to receiver. The goal of the protocol is for sender to send 2 classical bits of information to receiver using his/her qubit. But before he/she does, sender needs to apply a set of quantum gates to his/her qubit depending on the 2 bits of information sender wants to send. Thus if the sender wants to send a 00, he/she does nothing to the qubit (apply the identity (I) gate). If wants to send a 01, then applies the X gate. Depending on what the sender wants to send, the sender applies the appropriate gate, then sends the qubit to the receiver for the final step in the process.

## Sender can manipulate h(is/er) part of entangled qubits to encode 2 bits of classical information
def state_00(qc):
pass
def state_01(qc):
qc.z(0)
def state_10(qc):
qc.x(0)
def state_11(qc):
qc.x(0)
qc.z(0)
def encoding(qc):
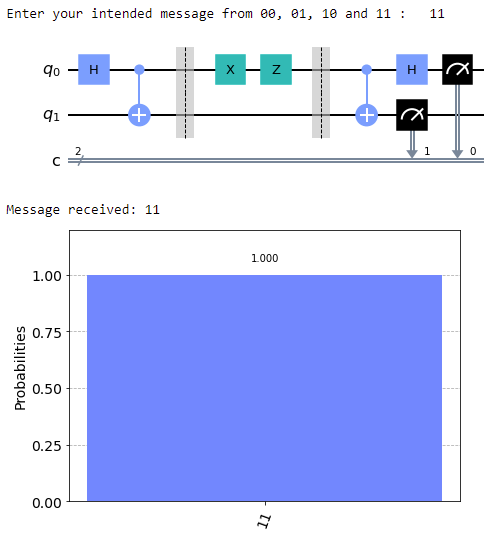
message = input('Enter your intended message from 00, 01, 10 and 11 : ')
if message == '00':
state_00(qc)
elif message == '01':
state_01(qc)
elif message == '10':
state_10(qc)
elif message == '11':
state_11(qc)
else:
print('Invalid message: Sending 00')
Sender sends h(is/er) encoded qubit physically to receiver.
def transmission(qc):
qc.barrier()
The receiver receives the sender's qubit (leftmost qubit) and uses his qubit to decode the sent message. Notice that he/she does not need to have knowledge of the state in order to decode it — he/she simply uses the restoration operation. The receiver applies a CNOT gate using the leftmost qubit as control and the rightmost as target. Then he applies a Hadamard gate and finally performs a measurement on both qubits to extract transmitted message.
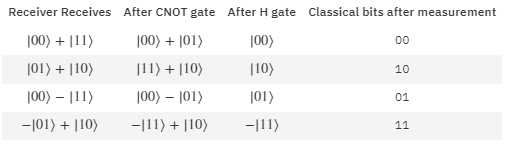
## Receiver bell-measures their qubits to retreive the encoded classical bits information:
def bell_measure(qc):
qc.cx(0,1)
qc.h(0)
qc.measure(range(2),range(2))
display(qc.draw('mpl'))
## Retrieving Information:
backend_sim = Aer.get_backend('statevector_simulator')
# backend_real_qc = least_busy(provider.backends(filters = lambda x: x.configuration().n_qubits >= 2
# and not x.configuration().simulator
# and x.status().operational == True))
# print("Running on: ", backend_real_qc)
# job = execute(qc,backend_real_qc)
job = execute(qc,backend_sim)
result = job.result()
counts = result.get_counts(qc)
received = dict([(value,key) for key,value in counts.items()])
print('Message received: {} '.format(received[1]))
display(plot_histogram(counts))
## Initializing:
qc_test = QuantumCircuit(2,2)
## Preparing entangled state:
preparation(qc_test)
## Sender Receiver moves apart:
seperation(qc_test)
## Sender encodes h(is/er) qubit according to intended 2 bits of classical information:
encoding(qc_test)
## Sender transmits h(is/er) encoded qubit physically to receiver:
transmission(qc_test)
# Receiver performs bell-measurement on both qubits to retrieve the encoded 2 bits of information:
bell_measure(qc_test)
About
Support
Every week, our team curates the most important news, events, and opportunities in the quantum space. Our subscribers gain early access to opportunities and exclusive interviews with prominent individuals. You don't want to miss out.